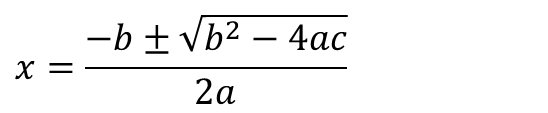公式暗記論vs公式導出論 優れているのはどっち？ | 淀川区 個別指導塾 淀川区三国の個別指導ならプレスト

公式をどう扱うか？

英単語や歴史用語なんかはこれはもう覚えるしかない。

関連付けはできるが、結局のところ知ってるか知らないかで、どれだけ計算してもマルクス＝アウレリウス＝アントニヌスは導けない。

しかし、数学や物理の公式はなんとか導ける。

そこで勃発するのが、「公式暗記論」vs「公式導出論」

まずは両者の意見を確認してみよう。

公式導出論者の主張

理系科目をやっていると必ず出現する公式暗記論。

とりあえず公式を覚えてしまえばいい！という主張をする。

丸暗記でテストに臨んでいる人も多く、文系にこの主張をする人が多いように思う。

実際、丸暗記でもある程度の点数が取れてしまうし、点数が取れるんだからそれでいいというのも、もっともだ。

学校によっては公式を書くというナゾの問題が出題されることすらある。

だったらコスパを重視して、変に考えるより丸暗記してしまう方が早い。

実に合理的だ。

公式導出論者の主張

公式暗記論の対極に位置するのが、公式導出論。

こちらはどちらかというと理系の人に多い。

かくいう僕も導出派だ。

公式は定義にしたがった結果なのだから、必ず導ける。

定義そのものは覚えるしかないが、公式を全て覚えることに比べたら大したことはない。

ちょっと考えたらわかることを丸暗記するなんてコスパ悪い。

実に合理的だ。

結局どっちがいいのか？

どちらもそれなりに言っていることは正しそうだが、結論をいうと

公式は覚えるしかない！

お前は導出論者だろうと突っ込まれそうだが、これは入試のシステムを考えると、もうしょうがない。

僕は指導する時には導出はするし、導出できると楽だともいう。

が、公式を毎回導出していたのでは、どうやったってテスト時間内に解き終わらない。

導出できるから大丈夫と言いつつ、結果的には公式を覚えてしまっている自分もいる。

これは公式導出論者のほとんどに当てはまることだと思う。

公式は導出が大事とか言いつつ、結局覚えちゃってるわけだ。

ということで、公式暗記論者の勝ち！

公式は使えているか？

とはいえ、暗記論者にこれだけは言っておきたい。

その丸暗記した公式は使えてるのか？

海外の学校では公式が問題文に書いてある事も多々ある。

つまり重視しているのは公式を”知っているか”ではなく、”使えるか”と言うことだ。

公式を使うというととりあえず代入することが思い浮かぶ。

例えばこの公式は知っているだろうか？

そう。２次方程式の解の公式。

これは超有名（というか基本中の基本）なのでみんな知っていると思うが、暗記派の人も導出派の人も意味が分かっていない人が結構多い。

例えば分母が０になる場合はどんな時ですか？

そういう事があり得るんでしょうか？

さらにもう一つ。

これはいわゆる判別式だが、これと解の公式の関係性が分かっていない人が意外と多い。

並べてみればすぐにわかることだが、丸暗記しようとすると関連付けができなくなってしまう。
（判別式は解の公式の√の中身。マイナスになったら、二次方程式の解が虚数になってしまう）

導出派の人は√の中身を判別式というということまでは分かっているが、中途半端な人はそれが何を意味するのかまで分かっていないので、結局役に立たないなんてことも。

結局何がいいたいかというと、暗記しようが、導出しようがなんでもいいから、その公式が何を意味するのかを理解しろ！ということだ。

丸暗記して、代入して終わりみたいな定期テストみたいな問題を突破できればいい！というのであれば、意味までは理解する必要はないかもしれない。

ただし、入試で使うのであれば、公式を使いこなせるようになるのは必須だ。

ど忘れの可能性も考えると単純な丸暗記はリスクが高すぎる。

公式を理解する方法

公式が何を意味しているのか理解するには、その公式の導出過程を追ってみるのが手取り早い。

なんでこんなことするんだろう？ということを考えながら導出過程を追っていくと、公式の中に出てるよくわからない項についても理解できるはずだ。

大事なのは「理解しようとする」こと。

導出は公式の意味を理解する上で役に立つが、ただ導出するだけでは何の意味もないということを知っておいてほしい。

導出過程を追っていくと、ややこしい計算だとか、そんな発想はムリ！ということになりかねないが、０から発想する必要はない。

意味を理解することが目的なのだから、すごい発想があるもんだな〜くらいのかんじで軽く流して、受け入れてしまおう。

意味が分かってくれば、わざわざ覚えようとしなくても、使っている内に自然と覚えてしまうものだ。

覚えなくてもいい公式

公式として習うものには何かしら意味があり、汎用性があるから公式として紹介されている。

汎用性の高いのは登場回数が多くなるので、自然と覚えられる。

逆を言えば、汎用性が低く、特定の条件下でしか使えない公式は覚える必要はないということだ。

便利だからということで紹介される公式（ヘロンの公式なんかは有名）は式自体から何を意味しているのか分かりにくいのでムリに覚えなくても大丈夫。
（もちろん意味を理解した上で、覚えられるなら覚えておくことに越したことはない）

なんとなくで覚えていると本番でミスるのが関の山だ。

ごく稀なケースを想定するより、汎用性が高い公式を確実に扱えるようにした方が、よっぽど得点アップに繋がる。

まとめ

公式を覚えるべきかについて話してきたが、公式は使えてなんぼ。

最低限覚える必要はあるが、ただ知っているだけでは意味がない。

なんのために公式があるのか考えて、きちんと使える形で覚えるようにしたい。

そのためには、一度導出過程を追ってみるのがいい勉強になる。

ただ、マニアックな公式まで全部覚えようとするとしんどいので、重要度が高く、出題頻度の高いものから順に覚えるようにしよう。